Atomic Physics #5
이전 포스팅에서 $\pi, \pi / 2$-pulse와 같은 single qubit operation에 대해서 알아보았다. 이번 포스팅에서는 two qubit operation에 대해서 알아보고자 한다. Classical computer의 CZ, CNOT Gate을 operate하는 법을 중점적으로 다루어보고자 한다.
7. Rydberg Blockade
우선 Rydberg atom에 대해 알 필요가 있다.
Definition. A Rydberg atom is an excited atom with one or more electrons that have a very principal quantum number.
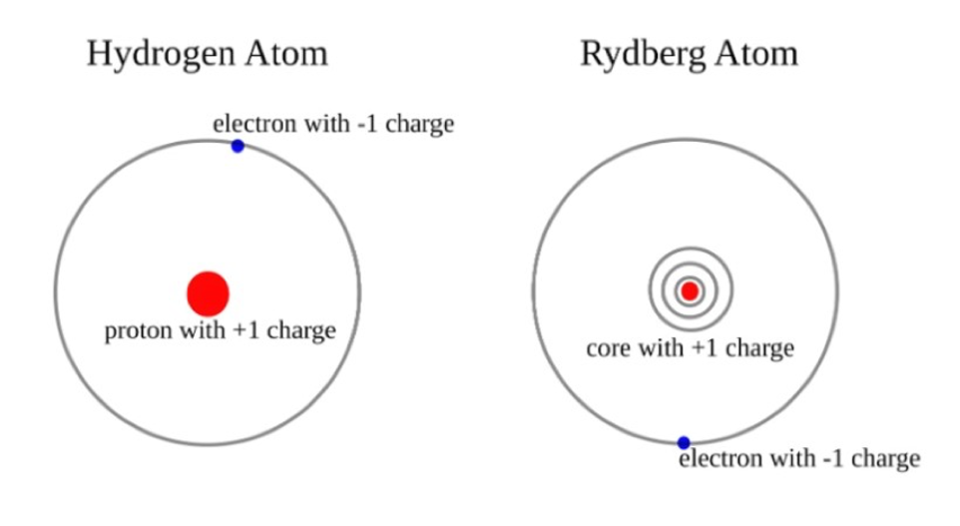
이와 같은 상태를 정의하는 이유는 앞으로 있을 gate operation에서 최외각껍질에 하나만 있어서, 마치 수소 원자와 같이 계산을 쉽게 하기 위함이다.

이전 포스팅에서 다루었던 trap들 중 하나들 이용해 atom들을 trap하고, trapped atoms 간의 거리가 충분히 가깝다고 하면 한 atom이 Rydberg atom이 되면 다른 atom의 에너지 준위는 이 영향을 받게 된다. 이를 perturbation theory를 이용해서 분석해보자.

고전 전자기학에서 dipole-dipole interaction은 아래와 같이 주어진다.
$$ V_{dd} = {1 \over 4 \pi \epsilon_{0}} { \vec{d}_{1} \cdot \vec{d}_{2} - 3 (\vec{d}_{1} \cdot \hat{r} ) ( \vec{d}_{2} \cdot \hat{r}) \over R^{3} }. $$
또한, two-body Hamiltonian은 아래와 같다. 이때 $\mathcal{H}_{dd}$는 perturbation term이다.
$$ \mathcal{H} = \mathcal{H}_{1} + \mathcal{H}_{2} + \mathcal{H}_{dd} $$
Perburtation theory에 의해,
$$ E_{dd}^{(1)} = \left\langle n' l', n' l' \right| \mathcal{H}_{dd} \left| n' l', n' l' \right\rangle = 0 $$
due to parity.
$$ E_{dd}^{(2)} = \underset{(n'', l''), (n''', l''') \neq (n', l')}{\sum} { |\left\langle \left\langle n' l', n' l' \right| \mathcal{H}_{dd} \left| n'' l'', n''' l''' \right\rangle \right\rangle|^{2} \over 2E_{n'l'} - E_{n''l''} - E_{n'''l'''} } \propto {n'' \over R^{6}}. $$
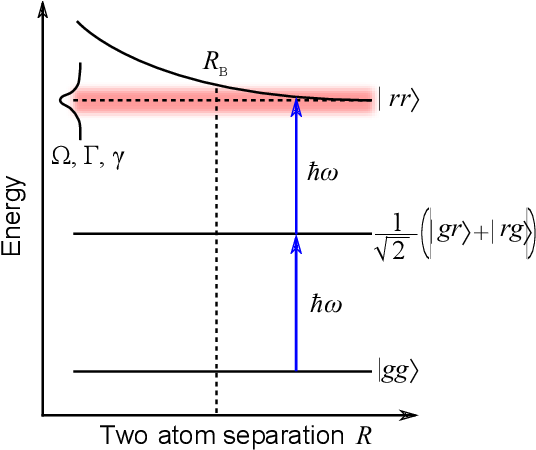
따라서 아래와 같은 energy diagram을 얻을 수 있다. 해당 diagram이 의미하는 바는, two atom system에서 한 전자가 $w$ frequency를 갖는 photon에 의해 $ \left| r \right\rangle$ $($Rydberg state$)$로 전이되었다면 다른 하나의 atom은 $r < R_{B} $에서는 더 이상, $w$ frequcncy를 갖는 photon에 의해서는 $\left| r \right\rangle$로 전이될 수 없음을 의미한다. 실제로 해당 전이에는 더 큰 에너지가 요구되기 때문에, 더 큰 $w'>w$가 요구된다. 이렇게 두 번째 전이가 차단되는 것을 Rydberg Blockade이다. 또한, 이는 조건부 연산으로 확장이 가능하기 때문에 gate operation의 좋은 도구가 된다.
8. Two Qubits Gate Operation
첫 번째로 CZ gate를 먼저 알아보자. Clasccial logic에서 CZ gate는 아래와 같이 정의된다.
$$ CZ = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & -1 \end{pmatrix}. $$
그렇다면 어떻게 이런 gate operation이 rydberg blockade를 이용해서 가능할까? 이는 이전 포스팅에서 서술한 pulse부터 시작한다. 이는 control과 target에 아래 figure와 같이 총 3번의 pulse를 제공해줌으로써 가능하다. 실제 계산은 많이 더럽지만, 아래 figure를 찬찬히 보면서 step by step을 밟아나가면 쉽게 이해할 수 있다. $($ 이 figure 찾는게 제일 어렵고 오래걸렸다... 이 figrue 찾고난 이후에는 시간 문제였지, 쉽게 이해했던 것 같다.$)$
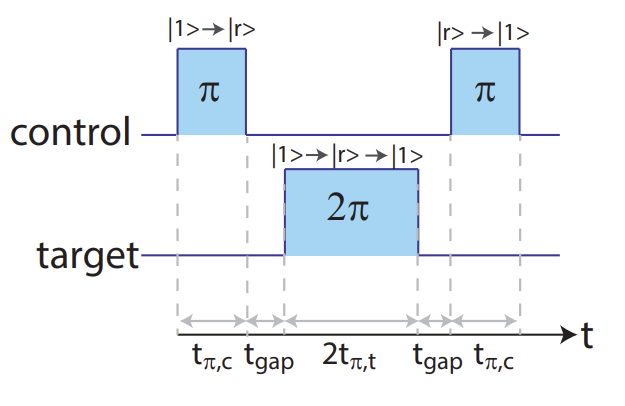

실제로 결과는 -CZ가 나오게 되는데, sign과 같은 global phase는 중요하지 않으므로 신경쓰지 않아도 된다. 이어서 Hadamard gate를 이용해서 CNOT gate를 만들어보자. Hadamard gate는 아래와 같다.
$$ H = {1 \over \sqrt{2}}\begin{pmatrix} 1 & 1 \\ 1 & -1 \end{pmatrix}. $$
Hadamard gate를 그대로 가져와서 target에만 작용하도록 할 수 있다. 그러면 $H_{tar}$은 아래와 같다.
$$ H_{tar} = \begin{pmatrix} H & O \\ O & H \end{pmatrix}.$$
그러면 끝났다!
$$ CNOT = H_{tar} \cdot CZ \cdot H_{tar} = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & 1 & 0 \end{pmatrix}. $$
그런데 $H$가 Rydberg blockade로 구현이 가능하냐고 묻는다면, 예리한 질문이다. 혹시 여기에 찜찜함을 느낀다면, 아래와 같은 5-pulse operation을 순차적으로 이행하면 된다. 그 결과는 아래와 같다.
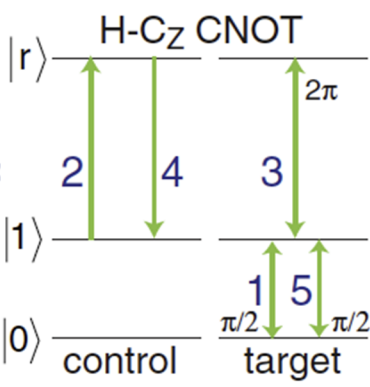
$$ CNOT = \begin{pmatrix} 1 & 0 & 0 & 0 \\ 0 & -1 & 0 & 0 \\ 0 & 0 & 0 & i \\ 0 & 0 & i & 0 \end{pmatrix}. $$
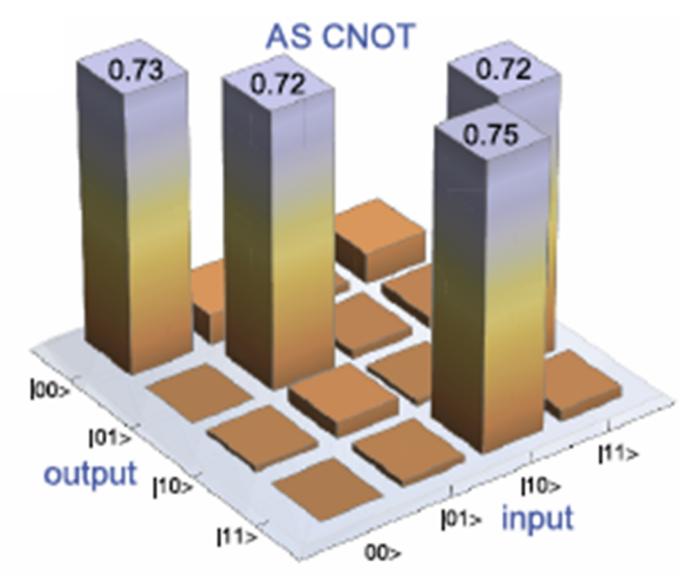
계수들이 기존과는 다르지 않냐고 묻는다면, 답은 상관없다. 왜냐하면 결국에는 해당 상태가 존재할 확률이 얼마인지가 관건인데 이들 값들은 모두 norm이 1이기 때문이다. 실제로 해당 과정을 수행한 논문의 결과를 첨부한다. 여기서 막대그래프의 높이는 fidelity를 의미한다.
9. Future Works
이제 이 이후의 내용들은 고체물리학, 2차 양자화 등의 과정을 거쳐 Boson-Hubbard Model, Fermi-Hubbard Model로 발전한다. 해당 이론들을 통해 상온 초전도체, 위상 부도체 등의 최신 양자물리 현상들을 시뮬레이션 할 수 있다고 한다. 뭐 자세한 건 나도 잘 모르겠지만, 재밌는 것 같으니 앞으로도 계속 공부하고 시간이 되면 포스팅 해보도록 하겠다!
길고 긴 과정이 이제 끝났다. 교수님의 표현을 인용하자면, 지금까지 배운 것은 classical comupter에서 기본 logic들을 어떻게 사용할 수 있는 것을 배운 것이고, 이제 이 이상의 연산들은 소프트웨어의 영역, 즉 코딩의 영역이라고 한다. 그래도 짧은 시간이지만, 오랜 기간 동안 겉핥기로만 알고 있던 Bloch sphere가 정확히 뭘 의미하는지 알 수 있었고, 특정 operation들이 Bloch sphere 위에서 어떻게 주어지는지 파악함으로써 single qubit operation 분석을 쉽게 할 수 있었다. 그 대표적인 예시가 바로 Rabi oscillation이다. 그리곤 single qubit operation과 rydberg atom을 기반으로 해서 two qubit operation인 CZ, CNOT gate까지 이해할 수 있었다. 이전에 배웠던 초전도 기반 양자컴퓨터는 초전도체를 잘 몰라서 고체물리를 아직 안배우기도 해서 이론적 기반이 좀 부족해서 혼자 논리를 펼쳐나가고 이해하는게 힘들었는데, 이번 이온 트랩 양자컴퓨터는 비교적 수식들이 친숙해서 시간을 쏟아부으면 이해가 잘 됐던 것 같다.
이번에는 공부하면서 논문들을 꽤 많이 읽고 공부했는데, 최신 논문들도 있고 이해도 어느 정도 되고 그래서 좀 좋은 것 같다. 앞으로도 물리학 쪽 논문들 읽을 일이 많은텐데 잘 이해됐으면 좋겠다.
그리고 여기서 bloch sphere representation의 representation이 내가 지금 공부하고 있는 표현론의 representation인가 하는 깊은 고민과 의심이 드는데, 이것은 표현론 혹은 물리에 대한 조예가 깊어지만 따로 또 포스팅 해보도록 하겠다 : )
이 다음 강의는 이제 이런 gate들을 어떻게 조합하고 다룰 수 있는지 다루는 software 강의인데, 공부를 해서 이해를 좀 많이하면 더 포스팅 해보도록 하겠다.
Reference.
1. K.M.Maller, A Rydberg blockade CNOT gate and entanglement in a 2D array of nerutal atom qubits, p.2.
2. Xiao-Feng Shi, Quantum logic and entanglement by netural Rydberg atoms: methods and fidelity, p.18.
3. Daniel Barredo, Experimental investigations of the dipolar interactions between a few individual Rydberg atoms, p.12.
4. Lecture Note of Andreas Schindewolf at TU Munchen