현대대수학II 기말고사 대비 요약
시간은 또 흐르고 흘러 기말고사 기간이 되었다. 수학과 복수 전공을 하면서 대수를 한참 동안이나 안 들어서 대수는 도대체 언제 듣나 생각을 하고 있었는데, 겨울방학에 대수I을 1학기에는 대수II, 표현론까지 공부하게 되어버렸다ㅋㅋ 난데 없이 수학 과목 중에서 제일 많이 들은 과목이 대수가 되어버린 셈이다... 그래도 인내심을 갖고 이해하려고 노력하면 이해가 크게 안되는 개념은 잘 없었던 것 같다. 이미 위상이랑 해석학에서 혼이 크게 나서 그런 걸지도... 체감 난이도는 대수<위상<<<해석학 정도인 듯 하다. 그런데 이 순서는 아이러니하게도 수강 순서의 역순이다ㅋㅋㅋ 심지어 해석학은 수학과 과목다운 첫 강의였다. 이런 걸 보면 수학과로 들어오는 진입 장벽을 하나 넘은 것 같기도 하다. 이정도 공부했으면 앞으로 대수 공부할 일은 한동안 없지 않을까... 새로운 개념을 배울 일은 잘 없지 않을까 싶다.$($ 사실 바람이다.$)$ 그래도 군, 환이라는 개념에 많이 익숙해진 듯 하다.
대수를 공부하면서 좋았던 점은 하나의 집적된 목표가 존재했다는 것이다. 바로 갈루아 이론이다. 갈루아 이론을 배우기 위해 정의, 정리들이 전개되고 이들이 집적되어 갈루아 이론이 증명된다. 다른 과목들은 그냥 허허벌판의 높이를 높이는 느낌이라면, 대수는 첨탑을 쌓아가는 느낌이었다. 공부를 해나가서 마지막 챕터에 도달해 갈수록 절정에 도달하고 있다는 느낌이 강하게 들었고, 이러한 느낌이 신기하고 공부를 재밌게 해주었던 것 같다. 비록, 갈루이 이론은 생각보다 싱겁게 증명되고 말지만... 아무튼 대수를 공부하면서 느낀 감정을 같이 공유해보자!
PART VII: Advanced Group Theory
Chp34: Isomprhism Theorems
Theorem 34.2$($First Isomorphism Theorem$)$:
Let $\phi : G \rightarrow G'$ be a homomorphism with kernel $K$, and let $\gamma_{K} : G \rightarrow G/K$ be the canonical homomorphism. Then $^{\exists !}$ an isomorphism $\mu G/K \rightarrow \phi[G] \ s.t.\ \phi (x) = \mu( \gamma_{K} (x))$ for each $x \in G$.

Lemma 34.3:
Let $N \triangleleft G$ and let $\gamma : G \rightarrow G/K$ be the canonical homomorphism. Then the map $\phi$ from the set of normal subgroups of $G$ containing $N$ to the set of normal subgroups of $G/N$ given by $\phi (L) = \gamma [L]$ is bijective.
Definition:
$ HN \equiv \{hn \mid h \in H, n \in N \}$
The join of $H$ and $N$ is the intersection of all subgroups of $G$ that contain $HN$.
Lemma 34.4:
$N \triangleleft G, H \le G \Rightarrow H \lor N = HN = NH.$
Furthermore, $H \triangleleft G \Rightarrow HN \triangleleft G.$
Theorem 34.5$($Second Isomorphism Theorem$)$:
$H \le G, N \triangleleft G \Rightarrow (HN)/N \cong H/(H \cap N).$
Theorem 34.7$($Third Isomorphism Theorem$)$:
$H, K \triangleleft G, K \le H \Rightarrow G/H \cong (G/K)/(H/K).$
Chp35: Series of Groups
Definition:
A subnormal$($or subinvariant$)$ series of a group $G$ is a finite sequence $H_{0}, H_{1}, \ldots, H_{n}$ of subgroups of $G$ $s.t. H_{i} \triangleleft H_{i+1}$ with $H_{0} = \{e\}$ and $H_{n}=G$.
A normal$($or invariant$)$ series of a group $G$ is a finite sequence $H_{0}, H_{1}, \ldots, H_{n}$ of normal subgroups of $G$ $s.t. H_{i} < H_{i+1}$ with $H_{0} = \{e\}$ and $H_{n}=G$.
Definition:
A subnormal$($normal$)$ series $\{K_{j}\}$ is a refinement of a subnormal$($ or normal$)$ series $\{H_{i}\}$ of a group $G$ if $\{H_{i}\} \subseteq \{K_{j}\}$.
Definition:
Two subnormal$($normal$)$ series $\{H_{i}\}$ and $\{K_{j}\}$ of the same group $G$ are isomorphic if there exists a one-to-one correspondence between the collections of factor groups $\{H_{i+1}/H_{i}\}$ and $\{K_{j+1}/K_{j}\}$ $s.t.$ corresponding factor groups are isomorphic.
$\Rightarrow$ Clearly, any two isomorphic subnormal$($normal$)$ series must have the same number of groups.
Lemma 35.10$($Zassenhaus Lemma$)$:
Let $H, K \le G, H^{*} \triangleleft H, K^{*} \triangleleft K$, then
$($i$)$ $H^{*}(H \cap K^{*}) \triangleleft H^{*}(H \cap K).$
$($ii$)$ $K{*}(H^{*} \cap K) \triangleleft K^{*}(H \cap K).$
$($iii$)$ $H^{*}(H \cap K)/H^{*}(H \cap K^{*}) \cong K^{*}(H \cap K)/K^{*}(H^{*} \cap K) $
$\qquad\qquad\qquad\qquad\qquad\qquad\ \ \cong (H \cap K)/\left[ (H^{*} \cap K)(H \cap K^{*}) \right].$

Figure is the subgroup diagram where $L = (H^{*} \cap K)(H \cap K^{*})$.
Theorem 35.11$($Schreier Theorem$)$:
Two subnormal$($normal$)$ series of a group $G$ have isomorphic refinements.
Definition:
A subnormal series $\{H_{i}\}$ of a group $G$ is a composition series if all the factor groups $H_{i+1}/H_{i}$ are simple.
A normal series $\{H_{i}\}$ of a group $G$ is a principal or chief series if all the factor groups $H_{i+1}/H_{i}$ are simple.
Theorem 35.15$($Jordan-Holder Theorem$)$:
Any two composition$($principal$)$ series of a group $G$ are isomorphic.
Definition:
A group $G$ is solvable if it has a composition series $\{H_{i}\}$ $s.t.$ all factor groups $H_{i+1}/H_{i}$ are abelian.
Example 35.19:
The group $S_{3}$ is solvable, because the composition series
$$ \{e\} < A_{3} < S_{3} $$
has factor groups isomorphic to $\mathbb{Z}_{3}$ and $\mathbb{Z}_{2}$, which are abelian.
The group $S_{5}$ is not solvable, because the composition series
$$ \{e\} < A_{5} < S_{5} $$
and $A_{5}/\{e\}$, which is isomorphic to $A_{5}$, is not abelian.
$\Rightarrow$ This fact is closely connected with the fact that a polynomial equation of degree 5 is not in general solvable by radical, but a polynomial equation of degree $\le$ 4 is.
Chp36: Sylow Theorems
Let $X$ be a finite $G$-set. Recall that for $x \in X$, the orbit of $x$ in $X$ under $G$ is $Gx = \{ gx \mid g \in G \}$. Suppose that there are $r$ orbits in $X$ under $G$, and let $\{x_{1}, x_{2}, \ldots, x_{r}\}$ contain on element from each orbit in $X$. Then
$$ |X| = \underset{i=1}{\overset{r}{\sum}} |Gx_{i}|. $$
There may be one-element orbits in $X$. Let $X_{G} = \{ x \in X \mid gx =x$ for all $ g \in G \}$. Then
$$ |X| = |X_{G}| + \underset{i=s+1}{\overset{r}{\sum}} |Gx_{i}| $$
where $s=|X_{G}| $.
Theorem 36.1:
Let $G$ be a group of order $p^{n}$ and let $X$ be a finite $G$-set. Then $|X| \equiv |X_{G}|$ $($mod $p$$)$.
P.S. 최근에 Shor's algorithm을 공부해서 그런가... a의 주기가 p^{n}이 되도록 잡으면, 알고리즘 개선이 안되나?라는 이상한 생각이 들었다.
Definition:
Let $p$ be a prime. A group $G$ is a $p$-group if every element in $G$ has order a power of the prime $p$.
A subgroup of a group $G$ is a $p$-subgroup of $G$ if the subgroup is itself a $p$-group.
Theorem 36.3$($Cauchy's Theorem$)$:
Let $p$ be a prime. Let $G$ be a finite group and let $p \mid |G|$. Then $G$ has an element of order $p$ and, consequently, a subgroup of order $p$.
Corollary 36.4:
Let $G$ be a finite group. Then $G$ is a $p$-group iff $|G|$ is a power of $p$.
Definition:
$G_{H} = \{ g \in G | gHg^{-1} = H \}. $
The subgroup $G_{H}$ is the normalizer of $H$ in $G$ and will be denoted $N[H]$.
$\Rightarrow N[H]$ is the largest subgroup of $G$ having $H$ as a normal subgroup. $ \Rightarrow H \triangleleft N[H]$.
Lemma 36.6:
Let $H$ be a $p$-subgroup of a finite group $G$. Then
$$ (N[H]:H) \equiv (G:H) (mod \ p) $$
Corollary 36.7:
Let $H$ be a $p$-subgroup of a finite group $G$. Then
$$ p | (G:H) \Rightarrow N[H] \ne H. $$
Theorem 36.8$($First Sylow Theorem$)$:
Let $G$ be a finite group and let $|G| = p^{n}m$ where $n \ge 1$ and $p \nmid m$. Then
$($i$)$ $G$ contains a subgroups of order $p^{i}$ for each $1 \le i \le n.$
$($ii$)$ Every subgroup $H$ of $G$ of order $p^{i}$ is a normal subgroup of a subgroup of order $p^{i+1}$ for each $1 \le i \le n.$
$\Rightarrow$ 첫 번째 실로우 정리가 의미하는 바는 $|G| = p^{n}m$일 때, $p^{i}$ order를 갖는 $G$의 subgroup들이 존재해서 $\{H_{i}\}$ series를 구성하고, $H_{i} \triangleleft H_{i+1}$이기 때문에 $\{H_{i}\}$는 subnormal series이다.
Definition:
A Sylow $p$-subgroup $P$ of a group $G$ is a maximal $p$-subgroup of $G$.
$\Rightarrow$ $P$는 첫 번째 실로우 정리의 $\{H_{i}\}$에서 마지막인 $G$ 바로 직전의 order가 $p^{n}$인 subgroup을 가리킨다. 당연하게도 유일하지는 않고$($composition이 유일하지 않기 때문에$)$, 이들 간에는 모종의 관계가 존재하는데 이는 두 번째 실로우 정리에서 다루어진다.
Theorem 36.10$($Second Sylow Theorem$)$:
Let $P_{1}$ and $P_{2}$ be Sylow $p$-subgroups of a finite group $G$. Then $P_{1}$ and $P_{2}$ are conjugate subgroups of $G$.
$\Rightarrow \ ^{\exists} g \in G \ s.t.\ P_{1} = gP_{2}g^{-1}.$
반대로, $P$가 Sylow $p$-subgroup일 경우 $gPg^{-1}$도 Sylow $p$-subgroup이다. 그럼 이때 Sylow $p$-subgroup은 몇 가지 존재하는가? 이 대답은 세 번째 실로우 정리에 있다.
Theorem 36.11$($Third Sylow Theorem$)$:
$G$ is a finite group and $p | |G|$ $\Rightarrow$ #$($Sylow $p$-subgroup$)$ $\equiv 1 (mod \ p) $ and divides $|G|$.
$\Rightarrow$ 특정 $|G|$에서는 두 가지 조건을 모두 만족하는 수가 하나로 국한된다. 이는 군에 대한 정보가 order 뿐이더라도 Sylow $p$-subgroup에 대한 많은 정보를 알려준다.
Chp37: Application of the Sylow Theory
Theorem 37.1:
Every every finite $p$-group is solvable.
Theorem 37.4:
The center of a finite nontrival $p$-group $G$ is nontrivial.
Lemma 37.5:
Let $H, K \triangleleft G\ s.t.\ H \cap K = \{e\}$ and $H \lor K=G.$ Then $ G \cong H \times K$.
Theorem 37.6:
For a prime $p$, every group $G$ of order $p^{2}$ is abelian.
Theorem 37.7:
If $p$ and $q$ are distinct primes with $p<q$, then every group $G$ of order $pq$ has a single subgroup of order $q$ and this subgroup is normal in $G$. Hence $G$ is not simple.
If $q$ is not congruent to 1 modulo $p$, then $G$ is abelian and cyclic.
Lemma 37.8:
Let $H$ and $K$ are finite subgroups of a group $G$, then
$$ |HK| = {|H||K| \over |H \cap K|}. $$
Example 37.9:
No group of order $p^{r}$ for $r>1$ is simple, where $p$ is prime. For by First Sylow Theorem, such a group $G$ contains a subgroup of order $p^{r-1}$ normal in a subgroup of order $p^{r}$, which must be all of $G$.
Thus a group of order 16$(=2^{4})$ is not simple. It has a normal subgroup of order 8$(=2^{4-1})$.
Example 37.10:
Every group of order 15 is cyclic, abelian, not simple by Theorem 37.7.
Example 37.11:
No group of order 20$(=2^{2} \cdot 5)$ os simple. For such a group $G$ contains Sylow 5-subgroups in number congruent to 1 modulo 5 and divisor of 20, hence only one. This Sylow 5-subgroup is normal, since all conjugates of it must be itself by Second Sylow Theorem.
Example 37.12:
No group of order 30$(=2 \cdot 3 \cdot 5)$ is simple. It suffices to show that there is only one Sylow $p$-subgroup for some prime $p$ dividing 30. By Third Sylow Theorem, the number of Sylow 5-subgroups are 1 or 6, and the number of Sylow 3-subgroups are 1 or 10. Let suppose there are six Sylow 5-subgroups, and the intersection of any two of is a subgroup of each of order dividing 5 by Lagrange Theorem. 5 implies that they are same groups. Then intersection of any two is trivial, $\{ e \}$. Thus $G$ contains 24$(=6 \times (5-1))$ elements or order 5. Similarly, $G$ contains 20$(=10 \times (3-1))$. 24+20=44 is larger than $|G|$=30. Then there is a normal subgroup either of order 5 or order 3.
Example 37.13:
No group of order 48$(=2^{4} \cdot 3)$ is simple. By Third Sylow Theorem, $G$ has either 1 or 3 Sylow 2-subgroups of order 16$(=2^{4})$ If there is only one subgroup of order 16, it is normal in $G$. Done.
Let suppose there are 3 Sylow 2-subgroups of order 16 in $G$. Let $H$ and $K$ be two of them. Then $|H \cap K| = 8$ by Lemma 37.8. Then $H \cap K$ is normal in both $H$ and $K$ by First Sylow Theorem. Hence the normalizer of $H \cap K$,$N[H \cap K]$, contains both $H$ and $K$ and must have order a multiple > 1 of 16$(=|H|=|K|)$ and a divisor of 48 both by Lagrange Theorem. Then $N[H \cap K] = G$. By property of normalizer, $(H \cap K) \triangleleft G$. Done.
Example 37.14:
No group of order 36$(=2^{2} \cdot 3^{2})$ is simple. Such a group $G$ has either one or four subgroups of order 9. If ther is only one such subgroup, Done. If there are four such subgroups, let $H$ and $K$ be two of them. By Lemma 37.8 likewise Example 37.13, $H \cap K$ has at least 3 elements. Thus the normalizer of $H \cap K$, $N[H \cap K]$, has as order a multiple of > 1 of 0 and a divisor of 36 by Lagrange Theorem. Hence $|N[H \cap K]|$ = 18 or 36. If the order is 18, then $(G:N[H \cap K]) = 2$. As a result, $N[H \cap K] \triangleleft G$. If order is 36, then $(H \cap K) \triangleleft G$.
Example 37.15:
Every group of order 255$(=3 \cdot 5 \cdot 17)$ is abelian. By Third Sylow Theorem, such a group $G$ has only one subgroup $H$ of order 17. Then $G/H$ has order 15 and is abelian by Example 37.10. By Theorem 15.20, the commutator subgroup $C$ of $G$ is contained in $H\ (\because H \triangleleft H)$. Then $|C|$ = 1 or 17.
Third Sylow Theorem shows that $G$ has either 1 or 85 subgroups of order 3 and either 1 or 51 subgroups of order 5. Similarly, there is a subgroup $K$ having either order 3 or order 5 and normal in $G$. Then $G/K$ has either order $5 \cdot 17$ or $3 \cdot 17$. Both case $G/K$ is abelian by Theorem 37.7. Thus $C \le K$ and $|C|$ = 1 or 3 or 5.
Therefore, $|C|$ = 1, that is, $C= \{ e \}$.
$G/H$ is abelian, $C \le H \Rightarrow G/C$ is abelian.
$G/C \cong G$ is abelian.
Consequently, by The Fundamental Theorem 11.12, G is cyclic.
PART X: Automorphisms and Galois Theory
Chp52: Totally Inseparable Extensions
Definition:
A finite extension $E$ of a field $F$ is a totally inseparable extension of $F$ if $\{E:F\} = 1 < [E:F]$. An element $\alpha$ of $\bar{F}$ is totally inseparable over $F$ if $F(\alpha)$ is totally inseparable over $F$.
$\Rightarrow$ We already know that $\{F(\alpha):F\}$ is the number of distinct zeros of $irr(\alpha,F)$. Thus $\alpha$ is totally inseparable over $F$ iff $irr(\alpha,F)$ has only one zeros that is of multipulicity > 1.
Theorem 52.3:
If $K$ is a finite extension of $E$, $E$ is a finite extension of $F$, and $F<E<K$, then $K$ is totally inseparable over $F$ iff $K$ is totally separable over $E$ and $E$ is totally inseparable over $F$.
Corollary 52.4:
If $E$ is a finite extension of $F$, then $E$ is totally inseparable over $F$ iff each $\alpha \in E-F$ is totally inseparable over $F$.
Theorem 52.5:
Let $F$ have characteristic $p \ne 0$, and let $E$ be a finite extension of $F$. Then $\alpha \in E-F$ is totally inseparable over $F$ iff there is some integer $t \ge 1\ s.t.\ \alpha^{p^{t}} \in F$.
Furthermore, there is a unique extension $K$ of $F$, with $F \le K \le E, \ s.t.\ K$ is separable over $F$, and either $E=K$ or $E$ is totally inseparable over $K$.
Chp53: Galois Theory
Recall:
1. Let $F \le E \le \bar{F}, \alpha \in E, $ and let $\beta$ be a conjugate of $\alpha$ over $F$. Then there is an isomorphism $\psi_{\alpha, \beta}$ mapping $F(\alpha)$ onto $F(\beta)$ that leaves $F$ fixed and maps $\alpha$ onto $\beta$.
2. If $F \le E \le \bar{F}$ and $\alpha \in E$, then an automorphism $\sigma$ of $\bar{F}$ that leaves $F$ fixed must map $\alpha$ onto some conjugate of $\alpha$ over $F$.
3. If $F \le E$, the collection of all automorphisms of $E$ leaving $F$ fixed forms a group $G(E/F)$. For any subset $S$ of $G(E/F)$, the set of all elements of $E$ left fixed by all elements of $S$ is a field $E_{S}$. Also, $F \le E_{G(E/F)}$.
4. A field $E$, $F \le E \le \bar{F}$, is a splitting field over $F$ iff every isomorphism of $E$ onto a subfield of $\bar{F}$ leaving $F$ fixed is an automorphism of $E$. If $E$ is a finite extension and a splitting field over $F$, then $|G(E/F)| = \{E:F\}$.
5. If $E$ is a finite extension of $F$, then $\{E:F\}\ [E:F]$. If $E$ is also separable over $F$, then $\{E:F\} = [E:F]$. Also, $E$ is separable of $F$ iff $irr(\alpha,F)$ has all zeros of multiplicity 1 for every $\alpha \in E$.
6. If $E$ is a finite extension of $F$ and is a separable splitting field over $F$, then $|G(E/F)|=\{E:F\}=[E:F]$.
Definition:
A finite extension $K$ of $F$ is a finite normal extension of $F$ if $K$ is a separable splitting field over $F$.
Theorem 53.2:
Let $K$ be a finite normal extension of $F$, and let $E$ be an extension of $F$, where $F \le E \le K \le \bar{F}$. Then $K$ is a finite normal extension of $E$.
And $G(K/E)$ is precisely the subgroup of $G(K/F)$ consisting of all those automorphisms that leaves $E$ fixed.
Moreover, two automorphisms $\sigma$ and $\tau$ in $G(K/F)$ induce the same isomorphism of $E$ onto a subfield of $\bar{F}$ iff they are in the same left coset of $G(K/E)$ in $G(K/F)$.
Definition:
If $K$ is a finite normal extension of a field $F$, then $G(K/F)$ is the Galois group of $K$ over $F$.
Theorem 53.6:
Let $K$ be a finite normal extension of a field $F$, with Galois group $G(K/F)$. For a field $E$, where $F \le E \le K$, let $\lambda(E)$ be the subgroup of $G(K/F)$ leaving $E$ fixed. Then $\lambda$ is a one-to-one map of the set of all such intermediate fields $E$ onto the set of all subgroups of $G(K/F)$. The following properties hold for $\lambda$.
1. $\lambda(E) = G(K/E)$.
2. $E = K_{G(K/E)} = K_{\lambda(E)}$.
3. $H \le G(K/F) \Rightarrow \lambda (K_{H}) = H$.
4. $[K:E]=|\lambda(E)|$ and $[E:F]=(G(K/F):\lambda(E)).
5. $E$ is a normal extension of $F$ iff $\lambda(E) \triangleleft G(K/F)$.
$\lambda(E) \triangleleft G(K/F) \Rightarrow G(E/F) \cong G(K/F)/G(K/E)$.
6. The diagram of subgroups of $G(K/F)$ is the inverted diagram of intermediate fields of $K$ over $F$.
Definition:
The Galois group $G(K/F)$ is the group of the polynomial $f(x)$ over $F$ where $K$ is a normal extension of $F$.
Theorem 53.7:
Let $K$ be a finite extension of degree $n$ of a finite field $F$ of $p^{r}$ elements. Then $G(K/F)$ is cyclic of order $[K:F]$, and is generated by $\sigma_{p^{r}}$, where for $\alpha \in K$, $\sigma_{p^{r}}(\alpha) = \alpha^{p^{r}}$.
Chp54: Illustrations of Galois Theory
Definition:
An element of the field $F(y_{1}, \ldots, y_{n})$ is a symmetric function in $y_{1}, \ldots, y_{n}$ over $F$, if it is left fixed by all permutations of $y_{1}, \ldots, y_{n}$.
Example 54.7:
Consider the splitting field of $x^{4}+1$ over $\mathbb{Q}$. We know that $x^{4}+1$ is irreducible over $\mathbb{Z}$. The work on complex number shows that the zeros of the polynomial are $(1 \pm i)/\sqrt{2}$ and $(-1 \pm i)/\sqrt{2}$.
Let
$$\alpha = {1+i \over \sqrt{2}}$$,
then
$$ \alpha^{3} = {-1+i \over \sqrt{2}}, \alpha^{5} = {-1-i \over \sqrt{2}}, \alpha^{3} = {-1+i \over \sqrt{2}}. $$
Thus the splitting field $K$ of the polynomial over $\mathbb{Q}$ is $\mathbb{Q}(\alpha)$, and $[K:\mathbb{Q}]=4$.
We can see that $G(K/\mathbb{Q}) \cong G_{8} = {1, 3, 5, 7}$ under multiplication modulo 8.
By simple algebraic calculation, we obtain two diagrams.
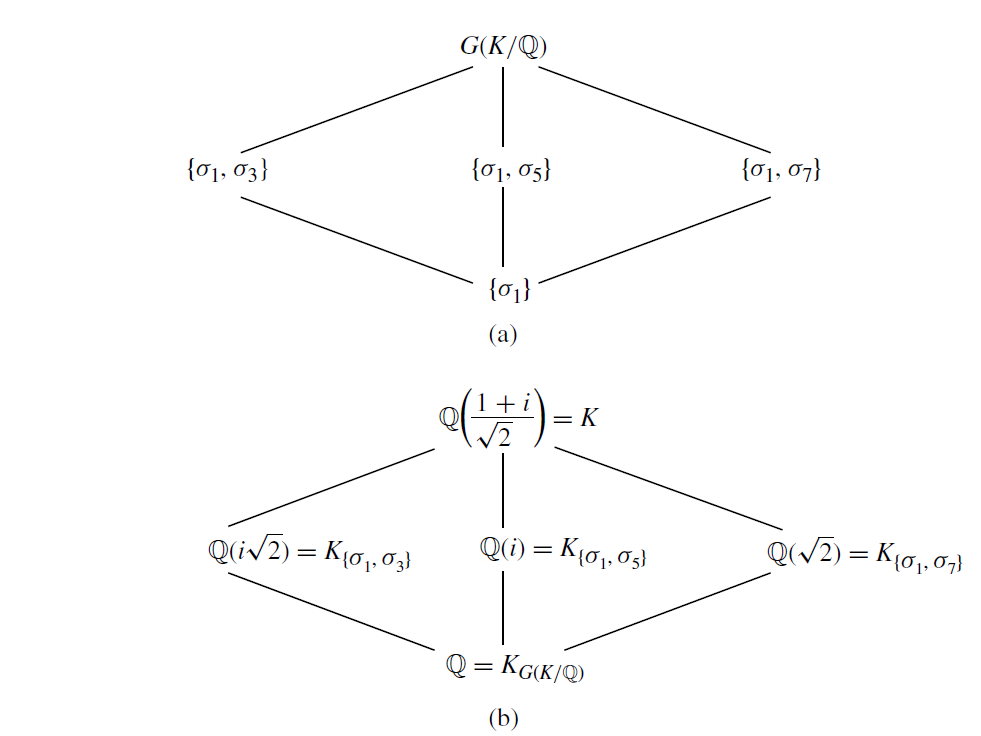
where
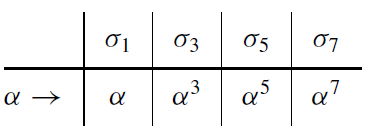
Chp55: Cyclotomic Extensions
Definition:
The splitting field of $x^{n}-1$ over $F$ is the $n$th cyclotomic extension of $F$.
$\Rightarrow$ the splitting field of $x^{n}-1$ is a separable and thus the splitting field is a normal extension of $F$.
Definition:
The polynomial
$$ \Phi_{n}(x) = \underset{\phi(n)}{\overset{i=1}{\prod}} (x - \alpha_{i}) $$
where the $\alpha_{i}$ are the primitive $n$th roots of unity in $\bar{F}$, is the $n$th cyclotomic polynomial over $F$ with $\phi(n)$ is Euler-phi function.
Theorem 55.4:
The Galois Griyo of the $n$th cyclotomic extension of $\mathbb{Q}$ has $\phi(n)$ elements and is isomorphic to the group consisting of the positive integers less than $n$ and relatively prime to $n$ under multiplication modulo $n$.
Example 55.5:
$x^{4}+1$ and $x^{8}-1$ both have same splitting field over $\mathbb{Q}$. This follows from the fact that $\Phi_{8}(x) = x^{4}+1$.
Corollary 55.6:
The Galois group of the $p$th cyclotomic extension of $\mathbb{Q}$ for a prime $p$ is cyclic of order $p-1$.
Constructible Polygons:
The regular $n$-gon is constructible $\iff$ $cos( 2 \pi /n )$ is constructible $\iff$ $\zeta + {1 \over \zeta} $ is constructible $\Leftarrow$ $[\mathbb{Q}(\zeta + {1 \over \zeta}): \mathbb{Q}]$ is power of 2
where $\zeta = cos(2 \pi /n) + i sin(2 \pi /n)$.
If $K$ is the splitting field of $x^{n}-1$ over $\mathbb{Q}$, then $[K:\mathbb{Q}]=\phi(n)$ by Theorem 55.4.
If $\sigma \in G(K/\mathbb{Q})$ and $\sigma(\zeta) = \zeta^{r}$, then
$$ \sigma(\zeta + {1\over \zeta}) = \zeta^{r} + {1 \over \zeta^{r}} = 2 cos({2 \pi r \over n} ). $$
$$ [ \mathbb{Q}(\zeta + {1 \over \zeta}) : \mathbb{Q} ] = { [K : \mathbb{Q}] \over [K : \mathbb{Q}(\zeta + {1 \over \zeta}) ] } ={ [K:\mathbb{Q}] \over |G(K/\mathbb{Q}(\zeta + {1 \over \zeta})) |} = { \phi(n) \over |\{\iota , \tau \}| } = {\phi(n) \over 2}$$
where $\tau(\zeta) = {1 \over \zeta}$.
Hence the regular $n$-gon is constructible only if $\phi(n)/2$ is a power of 2.
Let $n = 2^{\nu} p_{1}^{s_{1}} \cdots p_{t}^{s_{t}} \in \mathbb{N}$, where $p_{i} $ are the distinct odd primes dividing n, then
$$ \phi(n) = 2^{\nu-1} p_{1}^{s_{1}-1} \cdots p_{t}^{s_{t}-1} (p_{1}-1) \cdots (p_{t}-1). $$
If $\phi(n)$ is to be a power of 2, then $p_{i} = 2^{m} +1$ and $s_{i} = 1$ for all $i$.
If $m=qu$, where $q$ is an odd prime, $2^{m}+1 = (2^{u})^{q} +1$ is divisible by $2^{u}+1$.
$$ p_{i} = 2^{2^{k}}+1. $$
is called a Fermat prime.
For $k=0, 1, 2, 3, 4$ gives the primes 3, 5, 17, 257, 65537. For $5 \le k \le 19$ the integer is not a prime and for $k > 20$ is unknown.
Then there is a following Theorem.
Theorem 55.8:
The regular $n$-gon is constructible with a compass and a straightedge iff all the odd primes dividing $n$ are Fermat primes whose squares do not divide $n$.
Example 55.7:
The regular 7-gons is not constructible, since 7 is not a Fermat prime.
Similarly, regular 18-gon is not constructible, for while 3 is a Fermat prime, its square divides 18.
Example 55.9:
The regular 60-gons is constructible, since $60=2^{2} \cdot 3 \cdot 5$ and 3, 5 are both Fermat primes.
Chp56: Insolvability of the Quintic
Definition:
An extension $K$ of a field $F$ is an extension of $F$ by radical if there are elements $\alpha_{1}, \ldots, \alpha_{r} \in K$ and positive integers $n_{1}, \ldots, n_{r}$ $s.t.$ $K = F(\alpha_{1}, \ldots, \alpha_{r})$ and $\alpha_{1}^{n_{1}} \in F$ and $\alpha_{i}^{n_{i}} \in F(\alpha_{1}, \ldots, \alpha_{i-1})$ for $1 < i \le r$.
A polynomial $f(x) \in F[x]$ is solvable by radicals over $F$ if the splitting field $E$ of $f(x)$ is contained an extension of $F$ by radicals.
$\Rightarrow$ 마지막 문장인 "splitting field가 extension of $F$ by radicals에 포함된다."는 말의 의미는 zero들이 이루는 field가 사칙연산과, 유한제곱근으로 표현되는 체 내부에 포함된다는 의미이다. 이는 다른 말로, 이러한 $f(x)$의 경우 근의 공식이 있다는 말이다.
Lemma 56.3:
Let $F$ be a field of characteristic 0, and let $a \in F$. If $K$ is the splitting field of $x^{n}-a$ over $F$, then $G(K/F)$ is a solvable group.
Theorem 56.4:
Let $F$ be a field of characteristic zero, and let $F \le E \le K \le \bar{F}$, where $E$ is a normal extension of $F$ and $K$ is an extension of $F$ by radicals. Then $G(E/F)$ is a solvable group.
$\Rightarrow$ 앞선 series에서 정의했던 solvable group과 solvable by radicals이 어떻게 연결되는지를 보여준다. 예를 들어 어떤 $f(x) \in F[x]$의 갈루아 군이 solvable 하지 않다면, Theorem 56.4의 대우에 의해, splitting field를 포함하는 extension of $F$ by radicals은 존재하지 않는다. 이는 다시 말해, $f(x)$의 근은 사칙연산과 유한제곱근 만으로는 표현될 수 없다는 의미이고, 이는 곧 근의 공식이 존재할 수 없다는 말과 동치이다.
Theorem 56.6:
Let $y_{1}, \ldots, y_{5}$ be independent transcendental real numbers over $\mathbb{Q}$. The polynomial
$$ \underset{i=1}{\overset{5}{\prod}} (x-y_{i}) = x^{6} + \underset{5}{\overset{i=0}{\sum}} s_{5-i}x^{i} $$
is not solvable by radical over $F=\mathbb(s_{1}, \ldots, s_{5})$, where $s_{i}$ is the $i$th elementary symmetric function in $y_{1}, \ldots, y_{5}$.
$\Rightarrow$ We know that $G(E/F) \cong S_{5}$, which is not solvable. Hence, by Theorem 56.4, $f(x)$ is not solvable by radicals over $F$.r
$\Rightarrow$ It is evident that a generalization of these arguments shows that a polynomial of degree $n$ need not be solvable by radicals for $n \ge 5$.
$\Rightarrow$ 따라서 5차 이상의 방정식은 근의 공식이 존재하지 않는다! $\Box$
길고 긴 논의 끝에 5차 이상 방정식의 근의 공식이 존재하지 않음을 증명할 수 있었다. 이제 정리들의 전체적인 느낌은 복습했으니까 전체적으로 정리들 한 번 증명해볼만한거 다시 증명해보고, 과제 문제들 풀어보면서 대수 시험 공부 마무리 지어야겠다!
재밌는 과목이었고, 실제로도 재미있었다. 수없이 밀려들어오는 정의들에 정신을 잃을 뻔 했지만... 시간이 지나서 혹은 이해하려고 노력해서 정의들을 그대로 받아들일 수 있게 되니 이해가 크게 안되는 것은 몇몇 빼고는 잘 없었다. Fraleigh 책이 친절해서 그랬던 것 같다. 어쨌든, 아무튼 이제 대수는 안녕~~
Reference:
A First Course in Abstract Algebra International Edition, PEARSON