What is the Holonomy?

두 학기 전인가... 미분기하개론을 해석학이랑 같이 들으려고 했었다. 그런데 이런저런 이유로 미분기하는 수강하지 못했다. 그래서 미분기하를 배우고자 하는 생각은 늘 있었다. 가장 근본적인 이유는 tensor를 좀 공부하고 싶어서였지만, 물리 공부를 하면 할수록 뭔가 이 알듯말듯한 이 내용들이 미분기하에 나오는 것 같다는 느낌이 강렬하게 들었다. 

 

그러던 차에 multipole 관련 논문을 공부하는데 여기에 Wilson loop이 나왔다. Wilson loop은 또 뭔가... 좀 찾아보니 tangent bundle이 나온다. 그럼 또 tangent bundle은 또 뭔가... 미분기하 내용이다... 그렇게 미분기하를 좀 찾아보니 parallel transport를 공부했다. 그러고 보니 이 개념은 Aharonov-Bohm phase와 굉장히 닮았다. 편미분 방정식과 대수위상수학에서 homotopy를 공부했을 때 느낀 생각과 비슷했다. 그러고 보니 미분기하에서는 connection, curvature를 정의하는데 이거 berry phase에서 berry connection, berry curvature로 한 번 만났었다. 이거 참... multipole 공부하다가 1D di-atomic linear chain polarization에서 만난 berry phase로 돌아왔다. 최근에 하는 공부들이 괜히 이어져 있는 것 같다는 느낌을 받은게 아닌 것 같다.

 

 

 

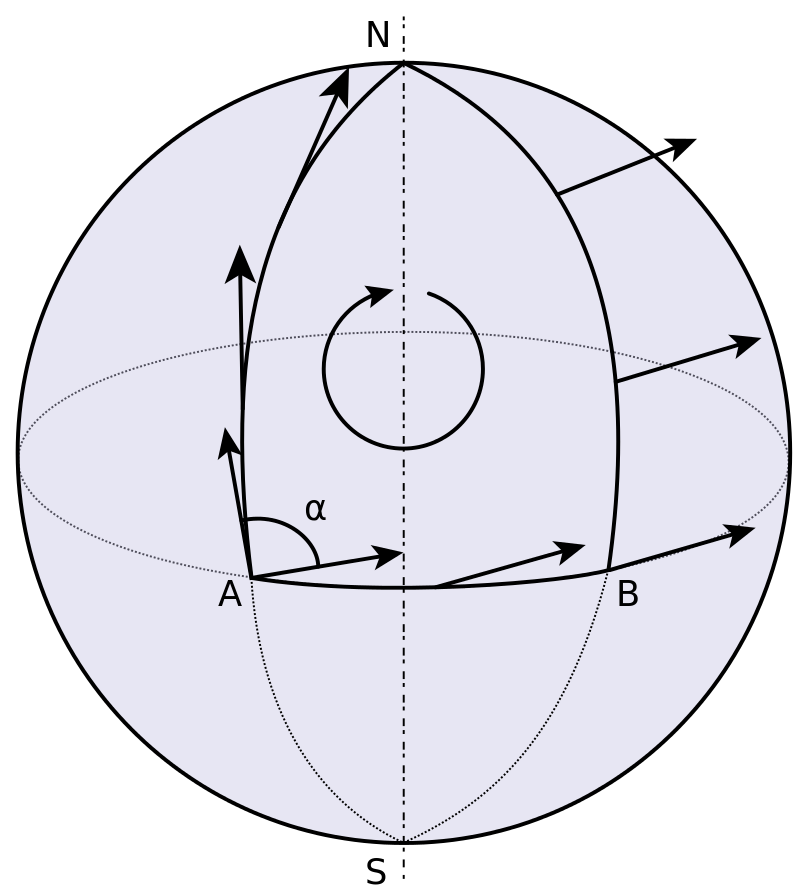
그래서 holonomy가 뭐냐 하면 한국 위키피디아 왈,

Definition:
미분기하학에서, 매끄러운 다양체 상에 주어진 코쥘 접속 또는 에레스만 접속의 홀로노미는 곡률의 존재로부터 나타나는 기하학적 결과로, 닫힌 곡선을 따라 평행 운송했을 때 기하학적인 정보가 변형되는 정도를 측정한 것이다.

라고 한다. 다른 건 다 필요 없고, 밑줄 친 내용이 핵심이다.

 

그래서 문득 든 생각이 기존에 솔레노이드에 자기장이 걸리지 않은 이중슬릿 실험은 Euclidean space라서 geometry phase를 변화시키지 않고, 자기장이 걸리게 되면 space가 non-Euclidean한 상태로 변형되어 holonomy가 발생되고 이게 geometry phase, 즉 berry phase가 아닐까 하는 생각이 들었다. 

뭐 아직은 manifold에 대한 정확한 정의조차 완벽하게 이해하지 못했으니 오류가 있을수도 있겠지만, 자기장이 기존의 공간의 변형시키고 이것이 non-zero holonomy를 만들어 phase 차이를 만들어내지 않을까라는 생각이다. 이것과 관련된 내용이 존재하는 것 같아서 공부를 좀 해봤는데 굉장히 재밌는 것 같다.  생각대로 흐름이 흘러가서 그런지 최근 중에 공부가 제일 재밌었다. 

그래도 수학을 배워둔게 많이 도움이 되는 것 같다. 예전에는 수학을 배우면 이걸 어디 써먹어?라는 생각이 많이 들었는데, 지금은 이게 수학이랑 관련이 있는거 같은데라는 생각이 들었을 때 관련된 수학이 정리되어 있으면 반갑고 고맙다ㅋㅋ 세상에는 참 똑똑한 사람들이 많다. 

 

아무튼 지금은 피곤해서 더 자세히 쓰지는 못하겠고... 공부를 좀 더 해서 답을 알게 되면 추가로 포스팅을 해보도록 하겠다. 생각한 추측이 맞았으면 좋겠다. 이제 좀 자야지...