Atomic Physics #4

6. Bloch Sphere Representation

Bloch sphere를 공부하기 이전에, 기초적인 양자역학 관련 정의들을 몇 가지 살펴보자.

 

Definition. The trace of an operator D is given by 

$$ Tr(D) \equiv \underset{n}{\sum} \left\langle n \left| D \right| n \right\rangle $$

where $\{ \left| n \right\rangle \}$ is a complete set of orthonormal eigenstates.

 

Definition. The density operator $\rho$ for the pure state $\left| \psi \right\rangle$ is given by

$$ \rho \equiv \left| \psi \right\rangle \left\langle \psi \right|. $$

 

The density operator offers useful tools such as calculating expectation value of operator $A$.

$$ Tr(\rho A) = Tr(\left| \psi \right\rangle \left\langle \psi \right| A) = \underset{n}{\sum} \left\langle n | \psi \right\rangle \left\langle \psi \right| A \left| n \right\rangle = \underset{n}{\sum} \left\langle \psi \right| A \left| n \right\rangle \left\langle n | \psi \right\rangle $$

$$ = \left\langle \psi \right| A \left( \underset{n}{\sum} \left| n \right\rangle \left\langle n \right| \right) \left| \psi \right\rangle = \left\langle \psi \right| A \left| \psi \right\rangle = \left\langle \psi \right\rangle. $$

In this case, completeness relation is used.

 

다시 돌아와서, 두 준위계의 파동함수는 다음과 같이 주어진다.

$$ \Psi(r,t) = c_{1} \left| 1 \right\rangle + c_{2} \left| 2 \right\rangle. $$

이때, density operator는

$$ \rho = \left| \psi \right\rangle \left\langle \psi \right| = \begin{pmatrix} c_{1} \\ c_{2} \end{pmatrix} \begin{pmatrix} c_{1} & c_{2} \end{pmatrix}^{*} = \begin{pmatrix} |c_{1}|^{2} & c_{1}c_{2}^{*} \\ c_{1}^{*}c_{2} & |c_{2}|^{2} \end{pmatrix} = \begin{pmatrix} \rho_{11} & \rho_{12} \\ \rho_{21} & \rho_{22} \end{pmatrix}.$$

여기서 $\rho$의 diagonal term은 populations, off-diagonal term은 coherences라고 불린다.

 

Let define $ \tilde{\rho}_{12} = \rho_{12} e^{-i \delta t}, \tilde{\rho}_{21} = \rho_{21} e^{i \delta t}$ where $\delta = w - w_{0}$,

$$ u = \tilde{\rho}_{12} + \tilde{\rho}_{21}, $$

$$ v = -i(\tilde{\rho}_{12}-\tilde{\rho}_{21}), $$

$$ w = \rho_{11} - \rho_{22}. $$

$u, v, w$에 각각에 시간에 대해 미분을 취하면

$$\dot{u} = \delta v ,$$

$$\dot{v} = -\delta u + \Omega w, $$

$$\dot{w} = - \Omega v.$$

이때 $c_{1}, c_{2}$에 대한 미분은 Rabi oscillation에서의 $c_{1}, c_{2}$ 관계식을 이용한다.

 

$R=(u,v,w)$으로 정의하고 위 미분을 정리하면$($계산이 굉~~~~장히 더러우므로 마음을 먹고 시작하자.$)$,

$$ \dot{\vec{R}} = (\dot{u}, \dot{v}, \dot{w}) = (\delta v, -\delta u + \Omega w, - \Omega v) = \begin{vmatrix} i & j & k \\ u & v & w \\ \Omega & 0 & \delta \end{vmatrix} = \vec{R} \times \vec{W} $$

where $ \vec{W} = (\Omega, 0, \delta).$

이때 $\vec{R}$을 Bloch vector라고 하고, $\vec{W}$는 Bloch sphere 상에서의 회전축을 의미한다.

 

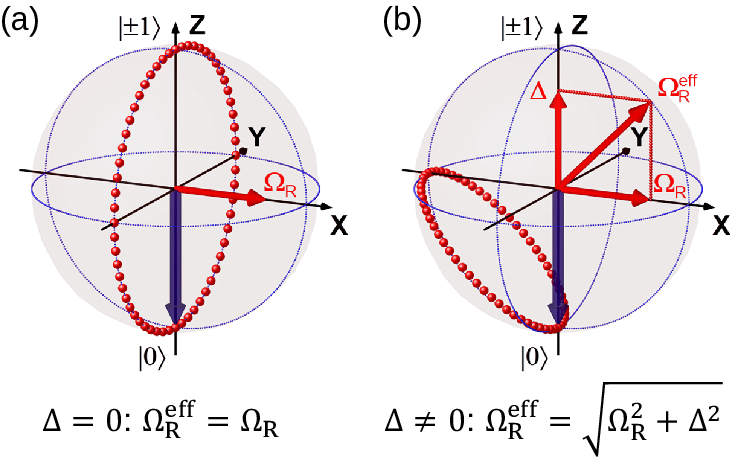
이처럼 Bloch sphere는 이준위 계에서 파동함수의 움직임을 매우 간결하고 명확하게 보여주는 강력한 도구로 사용된다. 따라서, Bloch sphere에 대한 이해는 양자컴퓨팅에서 gate operation이 어떻게 파동함수에 작용하는지 쉽게 파악하는데 사용된다.